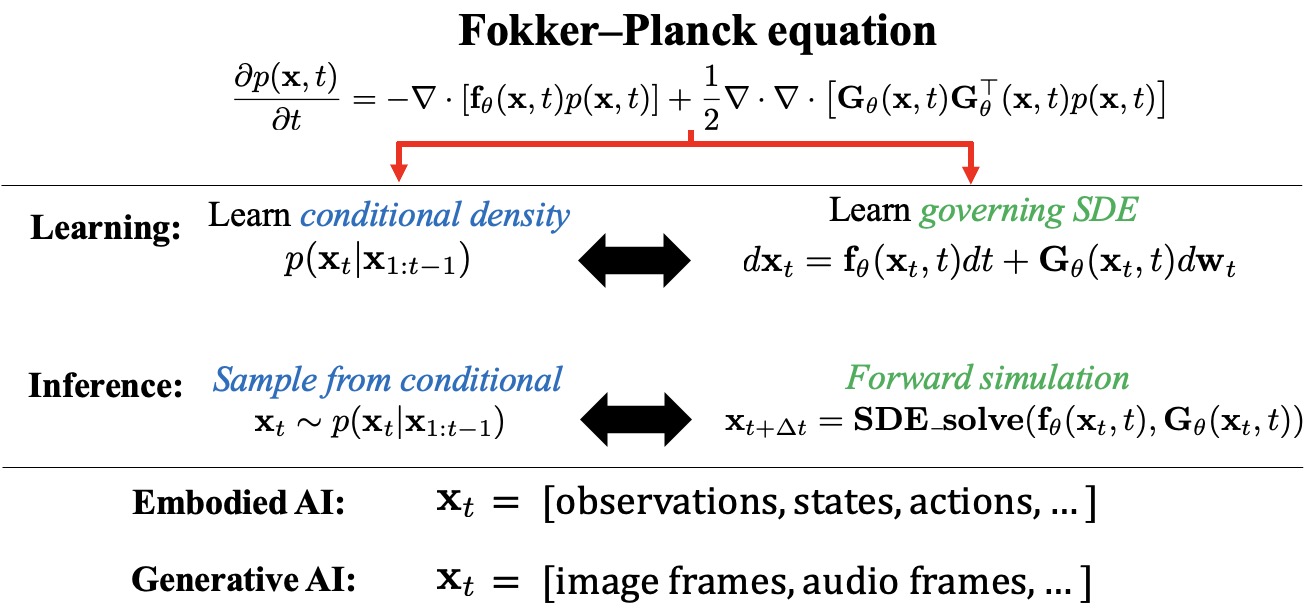
Inspired by the ubiquitous use of differential equations to model continuous dynamics across diverse scientific and engineering domains, we propose a novel and intuitive approach to continuous sequence modeling. Our method interprets time-series data as discrete samples from an underlying continuous dynamical system, and models its time evolution using Neural Stochastic Differential Equation (Neural SDE), where both the flow (drift) and diffusion terms are parameterized by neural networks. We derive a principled maximum likelihood objective and a simulation-free scheme for efficient training of our Neural SDE model. We demonstrate the versatility of our approach through experiments on sequence modeling tasks across both embodied and generative AI. Notably, to the best of our knowledge, this is the first work to show that SDE-based continuous-time modeling also excels in such complex scenarios, and we hope that our work opens up new avenues for research of SDE models in high-dimensional and temporally intricate domains.